“FEARS est une nouvelle méthode de classification de Séries Temporelles très efficace, exploitant de multiples représentations et capable d’extraire des descripteurs informatifs”
Qu’est-ce qu’une série temporelle ?
Une série temporelle est une suite de valeurs ordonnées dans le temps, c’est-à-dire une courbe. Comme illustrée par la Figure 1 ci-dessous, les valeurs d’une série temporelle sont généralement mesurées selon un pas de temps régulier (ex: toutes les secondes). Une série temporelle est définie sur une certaine période de temps, c’est-à-dire qu’elle comporte un nombre de valeurs fixé.
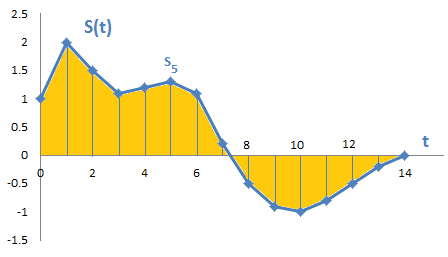
Figure 1 – Exemple d’une série temporelle S(t) consistant en une suite de valeurs <S1, S2 … > échantillonnées régulièrement selon le pas de temps T
Les séries temporelles sont un type de données très répandu dans le groupe Orange. Par exemple, le fonctionnement d’un serveur de vidéo à la demande (VOD) peut être caractérisé par plusieurs indicateurs mesurés au cours du temps, tel que l’usage des CPU, de la RAM, du réseau. Dans ce cas, on parle de séries temporelles multivariées, car plusieurs indicateurs sont mesurés à chaque pas de temps.
Quelles sont les tâches d’apprentissage possibles ?
La littérature sur les séries temporelles traite diverses tâches d’apprentissage, telles que la “prévision” qui consiste à prédire la suite d’une série temporelle (cf Figure 2(a)); ou encore le “clustering” qui regroupe les séries temporelles par paquets homogènes (cf Figure 2(b)). Dans ce billet, un focus est plus particulièrement mis sur la “classification” de séries temporelles, dont l’objectif consiste à assigner une série temporelle à l’une des classes présentes dans un ensemble prédéfini. La Figure 2(c) représente un problème de classification à deux classes représentées par les couleurs rouge et verte). Le modèle appris est matérialisé par un séparateur (la ligne orange en pointillés). L’objectif est donc d’apprendre un modèle capable de discriminer au mieux les deux classes.
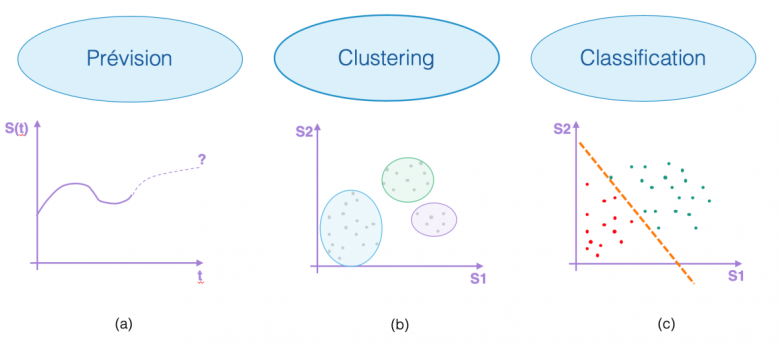
Figure 2 – Illustration des différentes tâches d’apprentissage.
Quels cas d’usage pour Orange ?
Les cas d’usage possibles dans le groupe Orange sont potentiellement nombreux. Ils ont été une source de motivation pour développer une nouvelle approche nommée FEARS. Par exemple, les cas d’usage de “maintenance prédictive” peuvent être posés sous la forme de problèmes de classification de séries temporelles. Reprenons l’exemple de notre serveur de VOD (cf. Figure 3). Un modèle de maintenance prédictive consisterait à prédire la classe 1 – signifiant “en panne dans 10 minutes” – ou 0 – signifiant “fonctionne correctement dans 10 minutes” – à partir des indicateurs (CPU, RAM et réseau) mesurés sur la dernière heure glissante. Une fois appris sur les données du passé, le classifieur sera capable de prédire en temps réel l’état de fonctionnement du serveur dans les 10 prochaines minutes à partir des indicateurs mesurés récemment.

Figure 3 – Maintenance prédictive sur un serveur de VOD
A la découverte des bonnes représentations et descripteurs
Au sein de la communauté scientifique, un consensus s’est dégagé sur le fait que, pour obtenir des classifieurs performants, il est nécessaire de transformer les séries temporelles, c’est-à-dire de passer du domaine temporel vers un espace de représentation alternatif. Il est également nécessaire d’extraire des descripteurs informatifs des séries pour faciliter l’apprentissage du classifieur. Ces descripteurs sont des valeurs qui caractérisent les séries temporelles (ex: l’écart type des points de mesure, la pente de la série…) et qui sont utilisés en entrée du classifieur. L’approche FEARS[1] propose d’automatiser ces deux étapes et de les réaliser conjointement.
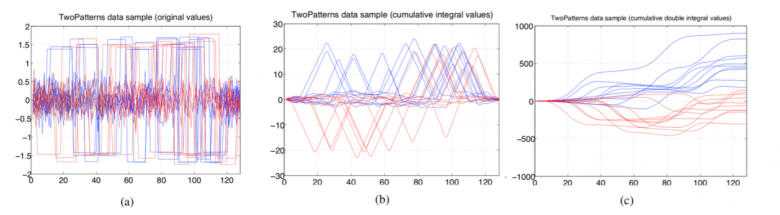
Figure 4 – Jeu de données “Two patterns” : représentation temporelle originelle ((a) à gauche), intégrale cumulée ((b) au centre), intégrale cumulée seconde ((c) à droite).
Pour illustrer l’importance de ces deux étapes, la Figure 4 montre l’exemple d’un jeu de données public nommé “two patterns” représenté selon plusieurs représentations. La Figure 4(a) montre les séries temporelles originelles représentées dans le domaine temporel. Dans ce cas, les deux classes (représentées pas les couleurs rouge et bleu) paraissent très difficiles à discriminer. La Figure 4(b) montre l’intégrale cumulée des mêmes séries temporelles. Le problème de classification devient alors beaucoup facile. Des descripteurs très informatifs peuvent être facilement extraits de cette représentation alternative. Par exemple, le fait de compter le nombre de valeurs supérieures à 10 ou inférieures à -10 constitue deux très bons descripteurs permettant au modèle de prédire les classes. La Figure 4(c) montre l’intégrale cumulée seconde de ces séries temporelles. Le problème de classification devient trivial car un simple seuil appliqué à la dernière valeur permet de discriminer parfaitement les deux classes. En pratique, le choix de la représentation et des descripteurs influent énormément sur la performance des classifieurs appris. L’approche FEARS a pour but d’automatiser ces choix.
L’approche proposée
Notre approche est capable d’extraire des descripteurs informatifs à partir des séries, tout en sélectionnant simultanément les représentations les plus utiles. Le lecteur intéressé trouvera de nombreux détails sur la méthode FEARS dans les articles scientifiques publiés : ([5], [6], [7]). La Figure 5 donne le fonctionnement général de la méthode et en montre les différentes étapes:
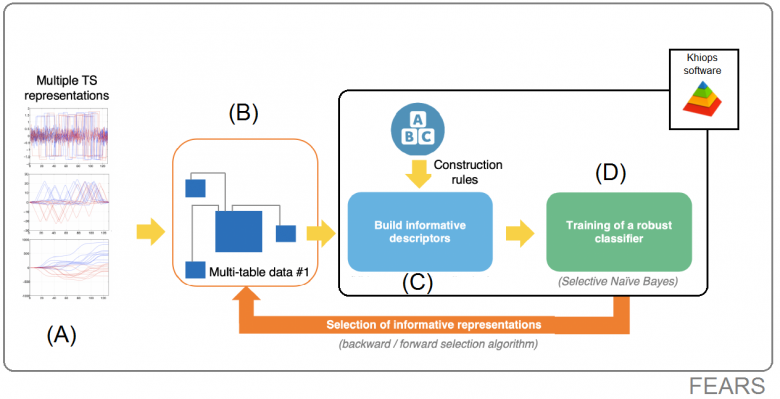
Figure 5 – Schéma fonctionnel de la méthode FEARS
(Partie A) : Les séries temporelles originales sont transformées en plusieurs représentations alternatives. Par défaut, sept représentations ont été choisies, tel que les dérivées, les intégrales, l’auto corrélation et la transformée de Fourrier. Mais le choix de ces représentations reste à la main de l’utilisateur final, parfois expert de son domaine applicatif.
(Partie B) : Ces différentes représentations sont stockées dans une base de données relationnelle. La table principale contient l’identifiant de chaque série, ainsi que la classe à apprendre (dans le jeu de données Two Patterns, il s’agite des classes rouge et bleue). Les tables secondaires contiennent les points de mesures pour chaque représentation des séries.
(Partie C) : Des descripteurs sont extraits des tables secondaires grâce à une méthode de “mise à plat” des données relationnelles (on parle de propositionalisation). Pour ce faire, le logiciel Khiops est utilisé et il permet de générer des descripteurs informatifs, sans risque de sur-apprentissage (i.e. apprentissage par cœur, qui ne se généralise pas).
(Partie D) : Un classificateur est ensuite appris en utilisant les descripteurs extraits comme données d’entrée.
(Flèche Orange) : Les étapes B, C, D sont répétées plusieurs fois, dans le but de sélectionner le meilleur sous-ensemble de représentations. En effet, une représentation peut s’avérer inutile pour certains jeux de données. Et le fait de conserver des tables inutiles dans les données relationnelles dégrade les performances du classifieur appris. C’est pourquoi à cette étape un algorithme de sélection de type “forward”[2] / “backward”[3] est utilisé.
Puisqu’il existe plusieurs façons d’encoder les différentes représentations dans un schéma relationnel (passage de la partie A à B) l’algorithme est exécutés deux fois, dans le but de tester deux schémas relationnels différents et de garder le meilleur.
L’approche proposée s’avère très compétitive par rapport aux méthodes de l’état de l’art, et extrait des descripteurs interprétables. De plus, FEARS est basée sur une formalisation originale, avec l’adoption d’une vision relationnelle rarement utilisée dans le domaine des Séries Temporelles. Cette approche est basée sur le framework mathématique MODL [8] qui est quasiment sans paramètres et nécessite peu de ressources matérielles du fait d’être implémenté au sein du logiciel Khiops issu des travaux de recherche d’Orange Labs.
Résultats
Des expérimentations ont été menées dans les articles [5] et [6]. FEARS a été challengé contre douze approches concurrentes et sur 85 jeux de données qui constituent un benchmark standard pour la communauté scientifique. Les résultats montrent que si le jeu de données contient un nombre suffisant d’exemples d’apprentissage [4] alors FEARS se situe sur le podium des trois meilleures méthodes de l’état de l’art.
Ceci est illustré par la Figure 6 où l’on voit les méthodes classées par leur rang moyen de performances sur les 85 jeux de données (à gauche la meilleure méthode, à droite la moins bonne). FEARS obtient la deuxième position sur les jeux de données testés. Le lecteur trouvera plus de détails dans [6] et pourra constater que FEARS présente également d’autres atouts : cette approche est particulièrement scalable et produit des résultats interprétables.
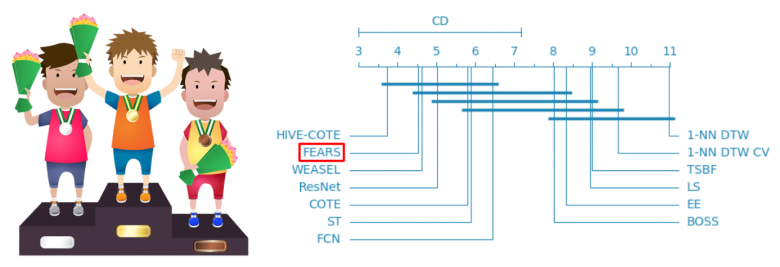
Figure 6 – Classement de la méthode FEARS vis-à-vis de 12 autres méthodes de l’état de l’art. FEARS est sur le podium des trois meilleures méthodes avec les méthodes HIVE-COTE et WEASEL. On trouvera une description des méthodes concurrentes (Hive-Cote, ResNet, 1-NN DTW) dans [5].
Perspectives, open challenge
Au carrefour des domaines des Séries Temporelles et de la fouille de données relationnelles, FEARS est une nouvelle méthode de classification de Séries Temporelles très efficace, exploitant de multiples représentations et capable d’extraire des descripteurs informatifs.
Les concepts clés de FEARS sont le stockage de représentations multiples de séries temporelles dans un schéma de données relationnel, la construction/sélection de descripteurs interprétables et la sélection de représentations. L’ensemble du processus permet d’obtenir des résultats très compétitifs en termes de précision par rapport aux meilleurs concurrents de l’état de l’art, à condition qu’il y ait suffisamment d’exemples d’apprentissage.
De plus, l’approche proposée permet d’extraire des descripteurs interprétables à partir des représentations sélectionnées, ce qui donne un compromis très avantageux entre (i) le temps de calcul, (ii) la précision des modèles appris et (iii) l’interprétabilité des descripteurs construits. Ainsi, FEARS peut être facilement utilisé dans un contexte industriel, en raison de son haut niveau d’automatisation, de performance et de facilité d’utilisation.
La vision relationnelle sur le domaine de la classification de séries temporelles offre une perspective naturelle pour les travaux futurs : le traitement de séries temporelles multivariées à haute dimension. Les tables secondaires du schéma relationnel pourraient stocker les nombreuses dimensions des séries multivariées. Il reste donc à trouver un moyen efficace et automatique de sélectionner les dimensions utile à la tâche d’apprentissage.
FEARS peut d’ores et déjà être utilisé dans les projets de Data Science, car une librairie python est disponible.
[1] FEature And Representation Selection approach for time series classification
[2] Cette stratégie part d’un ensemble vide. Les représentations sont ajoutées une à une. A chaque itération, la représentation optimale suivant un certain critère est ajoutée. Le processus s’arrête soit quand il n’y a plus de représentation à ajouter.
[3] Cette stratégie part de l’ensemble initial de représentation issue de l’étape forward. A chaque itération, une représentation est enlevée de l’ensemble. Cette représentation est telle que sa suppression donne le meilleur un meilleur nouveau sous-ensemble.
[4] C’est-à-dire plus de 500 séries temporelles, ce qui ne semble pas très grand à l’ère du big data.
[5] Gay, D., R. Guigourès, M. Boullé, et F. Clérot (2013). Feature extraction over multiple re-presentations for time series classification. In New Frontiers in Mining Complex Patterns -Workshop NFMCP 2013, ECML-PKDD 2013, Revised Selected Papers, pp. 18–34
[6] Bondu, A., D. Gay, V. Lemaire, M. Boullé, et E. Cervenka (2019). FEARS : a FEAture and representation selection approach for time series classification. In Proceedings of The 11th Asian Conference on Machine Learning, ACML 2019, Nagoya, Japan, November 17-19,2019., pp. 1–17.
[7] Gay, D., A. Bondu, V. Lemaire, M. Boullé, et F. Clérot (2020). Multivariate time series classification : a relational way. In International Conference on Big Data Analytics and Knowledge Discovery (DAWAK) 2020.
[8] Bondu, A., M. Boullé, et D. Gay. Data grid models, slides for the tutorial given at the conference “Extraction et Gestion des Connaissances” (EGC) 2013, Toulouse, France. http://www.marc-boulle.fr/publications/TutorialEGC13.pdf.
[9] Adeline Bailly, “Time Series Classification Algorithms with Applications in Remote Sensing”, PhD Thesis, Rennes, 2018